Competitive Performance of Elite Olympic-Distance Triathletes: Reliability and Smallest Worthwhile Enhancement Carl D Paton, Will G Hopkins Sportscience 9, 1-5, 2005
(sportsci.org/jour/05/wghtri.htm)
|
IntroductionAnyone with a serious interest in the performance of top-level athletes should appreciate the importance of the smallest worthwhile change in performance: the change that makes a meaningful difference to an athlete's chances of winning. Knowledge of this change is needed when assessing athletes with a performance test either to make decisions about meaningful changes in an individual or to research strategies that might affect performance (Hopkins, 2004). For athletes who compete as individuals and who win by achieving the best time, distance or other score, analysis of reliability (reproducibility or variability) of competitive performance provides an estimate of the smallest worthwhile change (Hopkins et al., 1999). Performance of the individual athlete always shows random variation from competition to competition. Enhancements or impairments of performance affect an athlete’s chance of winning only if they are greater than about half the magnitude of this random variation. As yet, the only fully published data on variability of competitive performance are for junior swimmers (Stewart and Hopkins, 2000), elite swimmers (Pyne et al., 2004) and non-elite runners (Hopkins and Hewson, 2001) More studies on the variability of competitive performance are needed. We address here the question of the magnitude of variability in performance time of top triathletes. MethodsWe
searched the Web for official result times of international Olympic-distance
triathlons. At the time, the practice of drafting (riding in packs during the
cycle stage) was not permitted. We arbitrarily limited data to the races in a
19-month period, as shown in Table 1.
To contribute to the analysis of reliability, athletes had to compete
in and finish at least two races. The
numbers of such athletes and their race times are shown in the table. For these athletes, overall mean times
(min) were: swim, 19.5; cycle, 59.8; run, 35.1; and total, 115.0. We
derived estimates of variability in times of individual athletes from race to
race using procedures described previously for competitive runners (Hopkins and Hewson, 2001). Briefly, we applied the
mixed linear modeling procedure (Proc Mixed) of the Statistical Analysis
System (Version 8.2, SAS Institute, Cary, NC) to log-transformed times and derived
a within-athlete coefficient of variation (standard deviation expressed as a
percent of the mean) along with their 90% likely (confidence) limits. The
within-athlete coefficient of variation represents the typical percent
variation in performance of an athlete from race to race after statistically
controlling for differences in mean times of each race.
The
above analyses were performed for all data and for subgroups of the top 10%,
20%, and 50% of the triathletes, identified by ranking the least-squares
means of each athlete's total time across all races. This ranking procedure adjusts each
athlete's race time for the mean duration of the race and for the races the
athlete did not enter, and thus it is a more accurate way to rank the
athletes than simply averaging raw times (Hopkins and Green, 1995). To examine
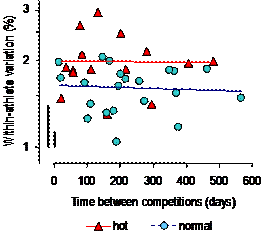
the effect of time between races on within-athlete variability, we computed
variability for every possible pairwise combination of races; we then plotted
the resulting coefficients of variation against the time between the
races. The effect of environmental
temperature on variability was investigated by labeling separately the points
on the plots representing races that were paired with one of the two races
held in the hottest conditions (>30°C, as provide in the official race results). Unweighted least-squares lines were fitted
to these points and to the points representing the pairs of all other
races. Confidence limits for these
lines and their comparisons were not derived, owing to the lack of independence
of the points. Differences
between coefficients of variation representing race-to-race variability were
considered substantial if their ratio was greater than 1.10. The rationale for this decision is as
follows: the smallest worthwhile
change in performance is proportional to the variability (Hopkins et al., 1999); sample size in studies aimed
at quantifying a mean change is inversely proportional to the square of the
magnitude of the change (Hopkins, 2000); therefore a ratio of 1.1
represents an increase in sample size of a factor of 1.21 (1.12),
or a 21% increase. ResultsTypical
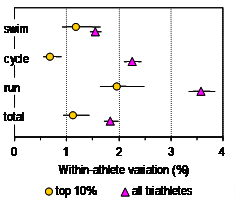
within-athlete variation in performance times from race to race is shown in
Figure 1. The variations in the figure
for all athletes are: swim, 1.6%; cycle, 2.3%; run, 3.6%; and total, 1.8%.
When combined independently or dependently, the variations of the three
phases yielded predicted variations in total time of 1.6% or 2.6%
respectively. Total
race time of the top 10% of athletes was 3.4% faster than that of the mean
for all athletes. For these top
athletes, the within-athlete variations shown in Figure 1 are: swim, 1.2%;
cycle, 1.3%; run, 2.5%; and total, 1.1%.
The predicted variations in total time were 1.0% or 1.6% respectively
for independent or dependent variabilities in the three phases. Variability
of performance of the top 20% of athletes was little different from that of
the top 10%, but the variability of the top 50% was substantially greater. Transition times were available for three venues (Table 2). Mean transition time was 89 s for the swim-cycle and cycle-run transitions combined. The between-athlete variation in time is equivalent to ~0.09% of the mean total race time of 115 min. Within-athlete variation over the three races was a little less (4.6 s, or 0.07%).
DiscussionWe performed this study primarily to determine the smallest worthwhile change in performance for top triathletes. The analyses also revealed interesting and useful information about the stability of performance time between races and about the contributions of each of the three phases and the transitions to performance time. The triathletes who were in the top 10% overall were substantially less variable in their performance than the average international triathlete. Less variability for faster subgroups of athletes in competitions has been observed in previous studies (Stewart and Hopkins, 2000; Hopkins and Hewson, 2001; Pyne et al., 2004) and presumably reflects more consistent preparation, pacing, or motivation from race to race. The smallest worthwhile change in performance is about half the typical race-to-race variation (Hopkins et al., 1999), so for our top triathletes this change is ~0.5×1.1 = 0.5% of total race time. A surprise finding was that random changes in times for each of the phases were largely independent of each other. It follows that any factors that normally affect a triathlete's performance in competitions must act predominantly in only one phase. For example, changes in endurance fitness, such as maximum oxygen uptake, either have a substantial effect on only one of the phases or are inconsequential on any phase relative to whatever other factors affect performance. It is therefore likely that any single strategy aimed at enhancing a triathlete's total performance time by the minimum target of 0.5% would have to focus on only a single phase. Before the recent change to permit drafting in the cycle phase, it was possible in principle to achieve the minimum gain of 0.5% in any phase; indeed, it may still be possible to achieve worthwhile gains in the swimming and cycling stages in a triathlon where a hilly course reduces the effect of drafting. The necessary gain in speed would depend on the duration of the phase. The duration of the swim phase is about one-sixth of the total duration, so a 0.5% enhancement in overall time would require a 3% (=6×0.5%) enhancement of swimming speed–an unrealistic target at the top level. Corresponding enhancements in cycling and running speeds would be 1.0% and 1.6%, which are more achievable. Now that drafting is allowed, it is reasonably clear that the medal winners have to leave the water in time to join the first cycling pack, because these riders generally stay together in the cycle phase and achieve a lead that is difficult for other riders to overcome in the running phase. The best triathletes therefore now have to be fast enough in the swimming phase to join the first pack in cycling phase, and they should focus performance-enhancing strategies on the run phase. If we assume that the only contribution to variation in total time now comes from the run phase, and that the within-athlete variation in the run phase of the top athletes is similar to what we observed (2.5%), the variation in total time becomes 35/115×2.5% = 0.8%; the smallest worthwhile change in total time becomes ~0.5×0.8 = 0.4%, and this change has to be achieved by a change of ~0.5×2.5% = 1.2% in running speed. There is also no substantial achievable gain in the transitions, because the variation in transition time represents <0.1% of the total time. In triathlons where drafting is permitted, the variation in the swim-cycle transition might be large enough in principle affect the athlete's chances of getting into the first pack. However, most of the variation in the transition is due to within-athlete random variation, and it is difficult to imagine how an athlete could modify such variation to improve a transition time. Another noteworthy finding is the remarkable stability of performance of triathletes at international level. Indeed, as can be seen in Figure 2, there was no indication in this sample of any increase in variability even over 19 months, implying that athletes hold their form for at least this period. The error bars in the figure show that the scatter in the within-athlete variation is due mainly to sampling variation in the estimates, rather than to true differences in variation between races. Finally, it is reasonably clear that performance was more variable for triathlons staged in the hottest conditions. The variability added by the heat is enough to substantially disadvantage some athletes relative to others. It is possible that aggressive acclimation strategies would reduce this variability to an inconsequential level, but some athletes may be inherently more disadvantaged in the heat, no matter how well acclimated they become. ReferencesHopkins WG (2000). Measures of reliability in sports medicine and science. Sports Medicine 30, 1-15 Hopkins WG (2004). How to interpret changes in an athletic performance test. Sportscience 8, 1-7 Hopkins WG, Green JR (1995). Combining event scores to estimate the ability of competitors. Medicine and Science in Sports and Exercise 27, 592-598 Hopkins WG, Hawley JA, Burke LM (1999). Design and analysis of research on sport performance enhancement. Medicine and Science in Sports and Exercise 31, 472-485 Hopkins WG, Hewson DJ (2001). Variability of competitive performance of distance runners. Medicine and Science in Sports and Exercise 33, 1588-1592 Pyne D, Trewin C, Hopkins W (2004). Progression and variability of competitive performance of Olympic swimmers. Journal of Sports Sciences 22, 613-620 Stewart AM, Hopkins WG (2000). Consistency of swimming performance within and between competitions. Medicine and Science in Sports and Exercise 32, 997-1001 Published Dec
2005 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||